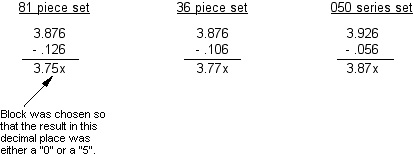BACK to
USE and CARE

How to Select Gage Blocks for Use
in Combinations

Gage block selection is a process that starts by examining the last or smallest decimal place
 of the desired combination and eliminating it while subtracting it from the remaining length of
 the desired combination as you proceed.  The process is repeated for each remaining decimal
 place until the total combination has been selected.

As an example:  A desired combination is to have a length 3.9762 in.

1)   Look over the available blocks in the set for a block that has a "2" in the fourth decimal
      place.   Most likely it will be a .1002" block.  (Some sets will have a .0502" block.)

2)  Subtract the selected block from the total length of the desired combination to eliminate the
     last decimal place.

3)  Now examine the next smallest decimal place.  (In this example, it ends with a "6".)  Find
     the blocks in the set that have a "6" in the third decimal place:

    If you are using an 81 piece set, choose the block that will leave either a "0" or a "5" in the
    second decimal place when you subtract this block from the result in Step 2.    (In this
    example, it would be the .126" block.)

4)  Subtract the selected block from the result in Step 2.

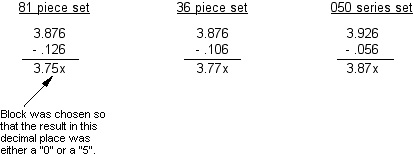5a)   If you are using an 81 piece set, the selection is about done.  It can be seen from the
        remainder in Step 4 above that a .750 and an 3.000 inch block will complete the
        combination.  Proceed to Step 10.

5b)  If you are using a 36 piece set or a .050 series set, you must continue to examine the
      smallest remaining decimal place of the result.   Choose the block in the set that will
      eliminate the last non-zero decimal place.  (In this example, the last decimal place
      contains a "7".)

6)  Subtract the chosen block from the remaining result in Step 4.

7)  Examine the last remaining non-zero decimal point.  Smaller sets do not usually have a .600
     or .800 inch blocks.   These sets usually contain these sizes:

                         .100
                         .200
                         .300
                         .400  (May or may not be included in the set)
                         .500

8)  Choose blocks from the series of blocks listed in Step 7 above that will add up to the
     remaining decimal place calculated in Step 6.  In this example, the choices would probably
     be:

     Note:  Other choices could be made as shown below.  But, it is recommended to keep the
     number of blocks in the combination as small as possible.  

9)  Now that all that remains is the whole number of inches in the combination.  (3 inches in the
     example.)  If the set has a single block of the desired length, choose it.  Otherwise, a
     combination of blocks will have to be selected.  In our example, it is more likely that the
     3-inch size will have to be built up from 1-inch and 2-inch blocks. 

10)  Double check the combinations by adding together all the selected blocks.

Metric gage block selection is performed in the same manner.  Always start with the last or
 smallest decimal place and eliminate it with your choice of blocks while you subtract it from
 the remaining length of the combination as you proceed.  Repeat this procedure until the total
 combination has been selected.

Example:  Desired combination length of 150.932mm

1)  Examine the blocks in the set that have a "2" in the third or lowest decimal point.

Choose: 

2)  Subtract the chosen block from the size of the desired combination.

3)  Choose a block to eliminate the next smallest non-zero decimal point.  If using an 88 or 112
     piece set, choose a block that will leave either a "0" or a "5" in this decimal place.

Choose: 

4)  Subtract the chosen block from the remainder in step 2.

5)  Choose block to eliminate the next smallest non-zero decimal point.  If using an 88 or 112
     piece set, choose a block that will eliminate the first whole millimeter decimal place as
     well.

Choose: 

6)  Subtract the chosen block from the remainder in step 4.

7) Choose blocks to equal the whole millimeters left in the combination.

8) Verify that the combination of chosen blocks equals the desired length. 

BACK to
USE and CARE

GB49