Webber Angle Gage Blocks permit fast, simple, and accurate measurement of angles. A set of
only 16 blocks will combine to make 356,000 different angles from 0° to 99° in steps of 1 second
to an accuracy of less than 1/1,000,000th of a circle.
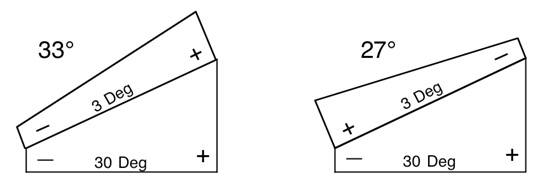
Their versatility derives from being able to use the blocks in combinations in either "plus" or
"minus" positions. For instance, to obtain an angle of 33°, take the 30° angle and add the 3°
angle, making sure that both the "plus" ends are together.
To make a 27° angle, you use the same two blocks but wring them together so that the "minus"
end of the 3° block is over the "plus end of the 30° block. This will subtract 3° from 30°, giving
the desired 27° angle.
|
|
|
|
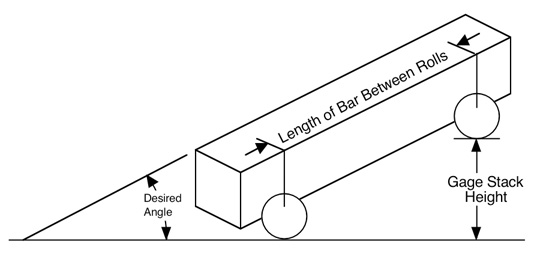
Webber Angle Gage blocks are more accurate and easier to use than a sine bar. Setting an angle
with a sine bar is more difficult to set because of the trigonometric formula that must be used.
For example, setting a simple 27° angle with a 5-inch sine bar:
1) Find sine of 27° = .453990499
2) Multiply by length of sine bar = 2.269952495
3) Round to closest .0001" 2.2700 (Closest combination with average set of blocks)
4) Calculate Size Error -0.000475 or -47.5µin. (Difference between Step 2 and Step 3.)
5) Calculate the Residual Angle Error: ≈ 2 arc seconds
Residual Angle Error = Calculated Size Error / 4.85 x Length of Bar
1 arc second = 4.85 microinches per inch. For a 5-inch sine bar: 1 second error = 24.25µin/in.
For the above example, the residual error would be 47.5µin / 24.25µin. or about 2 arc seconds.
Using a sine bar, a combination of 2.2700 inches must be built. For most sets, this would be a
combination of 3 blocks: 2-inch, .120", and .150"
With an Angle Gage Block set, only 2 blocks are required: 30° and 3° Subtracting the angles as
shown above. And, there is no residual error.
|
|
|